One of my extracurricular hobbies is science pedagogy, largely in the context of making physical sensing devices that make physical science easier to understand — like my open source science tricorder project, or the open source computed tomography scanner. I’ve been very much interested in starting a series of posts on explaining my recent past (and, future) research papers in plain language, both to make them more accessible for general readers, but also to make short, relatively quick, and equally accessible reads for my colleagues who (if they’re anything like me) have a long list of papers they’d like to read, and many demands on their precious research time.
With that, the inaugural post of Papers in Plain language —
Papers in Plain Language: What’s in an Explanation? Characterizing Knowledge and Inference Requirements for Elementary Science Exams. (Peter Jansen, Niranjan Balasubramanian, Mihai Surdeanu, and Peter Clark). Published at COLING 2016. The PDF is available here, and the associated data for the paper is available here.
Context: Why study science exams?
My primary research interests are in studying how we can teach computers enough language and inference to perform fairly complicated inference tasks (like solving science questions), and to do this in ways that are explainable — that is, that generate human-readable explanations for why the answers are correct. Unlike most AI researchers who are primarily interested in figuring out ways to get computers to perform adult-level tasks, I’m biased to believe that a better way of achieving cognitive-like abilities in artificial intelligence is to model how humans learn from the earliest ages. That’s why I went to graduate school to learn how to computationally model language development and knowledge representation developmentally, which is a cognitive term meaning as children learn to do.
Elementary science exams (to me) have this great capacity to study how we can teach computers to perform complex inference, because both the language understanding and complex inference tasks tend to be much simpler than what we see in adult-level tasks. That means we’re better able to distill the essence of the inference task, like peeling back the layers of an onion to get closer to looking at how the problem works, how well we’re doing currently, and what we don’t yet understand that would help us do better. That’s essentially what this paper is about — a detailed analysis of the knowledge and inference requirements to successfully answer (and explain the reasoning behind solving) hundreds of elementary science questions, using both existing methodologies (the “top-down” methodologies we’ll examine in a minute), and a new methodology — looking at the same questions “bottom-up” by building a large number of real and detailed explanations, and examining them to learn more about the nuts and bolts of these inference problems. We show that these old and new methods produce radically different results, and that you should definitely use the explanation-centered method if you’re able to devote the time to the analysis.
Top-Down Analysis
Before we (humans) can solve a question, we have to understand what the question is asking. Most of the time with automated methods of question answering, we do almost the opposite — we apply the same method of solving to all questions — because the science of understanding what a question is asking is still being developed. One of my favorite papers (A Study of the Knowledge Base Requirements for Passing An Elementary Science Test, Clark et. al, AKBC 2013) works on this problem by analyzing about 50 elementary science questions from the New York Regents 4th grade science exam, and uncovering 7 broad classes that those questions could be, as well as what proportion of questions belong to each class. Their figure with these classes and proportions is shown below:
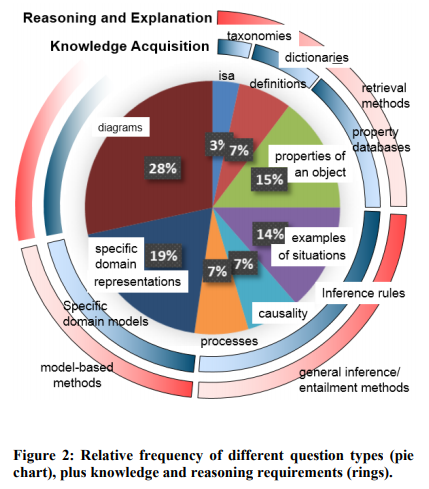Here we the 7 broad categories of questions that Clark et al. discovered — is-a questions, definition questions, questions that ask about properties of objects, questions that test examples of situations, questions that address causality or a knowledge of processes, and the last (and, arguably most complex) — domain specific model questions. But what do these mean? Clark et al.’s AKBC2013 paper is full of examples, easily digestible, and highly worth a read — here are a few of those examples.
- Taxonomic (is-a) questions test a knowledge that X is a kind of Y. For example, Q: Sleet, rain, snow, and hail are forms of: (A) erosion (B) evaporation (C) groundwater (D) precipitation
- Definition questions test a knowledge of the definition of concepts. For example, Q: The movement of soil by wind or water is called (A) condensation (B) evaporation (C) erosion (D) friction
- Property questions test knowledge that might be found in property databases. For example, part-of knowledge is tested by the following question, Q: Which part of a plant produces the seeds? (A) flower (B) leaves (C) stem (D) roots
The above question types can be thought of as “retrieval types”, in that they could be successfully answered by looking up the knowledge in a ready-made knowledge base. A more interesting (to me) subset of questions are those that appear to require forms of general or model-based inference, as in the examples below:
- Examples of situations, such as Q: Which example describes an organism taking in nutrients? (A) A dog burying a bone (B) A girl eating an apple (C) An insect crawling on a leaf (D) A boy planting tomatoes in the garden
- Causality, as in Q: What is one way to change water from a liquid to a solid? (A) decrease the temperature (B) increase the temperature (C) decrease the mass (D) increase the mass
- Simple Processes, which often appear related to causality questions, such as Q: One way animals usually respond to a sudden drop in temperature is by (A) sweating (B) shivering (C) blinking (D) salivating
- Domain Specific Models, that require reasoning over domain-specific representations and machinery to solve. For example, Q: When a baby shakes a rattle, it makes a noise. Which form of energy was changed to sound energy? (A) electrical (B) light (C) mechanical (D) heat
A Larger Top-Down Analysis
This analysis is really fascinating, because it gives a set of specific question types in the dataset, each of which requiring specific kinds of knowledge, and specific solving methods. In a way it helps serve as the beginnings of a recipe book for the problem of building question answering systems for this dataset — before reading the paper you’re likely in the paradigm of applying the same model to each question, but after reading Clark et al’s analysis you can begin to plot out how you might make specific solving machinery for each of these 7 questions, and how you need to get to work collecting or building specific knowledge resources (like a large taxonomy, or a part-of database, or a database that represents causal relationships) before you can make headway on certain classes of problems.
I wanted to do exactly that — and also, to automatically detect which question type a given question was, so that I could go about building a system to intelligently solve them. So I set out to perform a larger analysis on more questions, and make a much larger set of training data for this question classification task. That’s when things started to get especially interesting.
Above is the beginnings of that analysis — essentially repeating the Clark et al. (AKBC 2013) analysis, but on all 432 training questions from the AI2 Elementary questions set (a smaller subset of what is now known as ARC, the Aristo Reasoning Challenge), including 3rd to 5th grade questions drawn from standardized exams in 14 US states. By and large the proportions here are very similar to the original analysis (except that there appear to be more domain-specific model questions in the larger set). The really interesting part was the labeling process itself.
The trouble with top-down categories: They’re perfectly obvious, except when they’re not.
The New York Regents standardized exam is known for being a very well constructed exam, and each of the problems appear to be carefully designed to test very specific student knowledge and inference capacities. When looking at real questions from different exams, things tend to get a little murkier. For example, consider the following question:
Q: Many bacteria are decomposer organisms. Which of the following statements best describes how these bacteria help make soil more fertile?
- (A) The bacteria break down water into food.
- (B) The bacteria change sunlight into minerals.
- (C) The bacteria combine with sand to form rocks.
- (D) The bacteria break down dead plant and animal matter (correct answer).
Now ask yourself: Which of the 7 knowledge types does this question fit into?
Thankfully, the answer is perfectly obvious. Unfortunately, it’s obviously one category to one person, and obviously a different category to the next person.
The question might be labeled causal, because it asks “how … bacteria help make [cause] soil [to become] more fertile?“. But similarly, it might be thought of as a process question, because decomposers are a stage in the life cycle process, which is the curriculum topic this question would be found under. Except that decomposers are part of an ecosystem model of recycling nutrients back into the soil. But the question might more simply be solved by just looking up the definition of the word decomposer, which dictionary.com describes as “an organism, usually a bacterium or fungus, that breaks down the cells of dead plants and animals into simpler substances”. The high number of overlapping words between this definition and the question and correct answer would make it particularly amenable to simple word matching methods.
The problem, unfortunately, is that all of these labels are essentially equally correct. They’re each different ways of solving the problem, using different solving algorithms.
Changing the problem: Building explanations that answer questions and explain the reasoning behind the answer.
When reaching a stumbling block like this (and, the depressingly low performance on a question classification system that I achieved using these labels that wasn’t reported in the paper), it’s sometimes helpful to take a step back and see if the analysis can be reframed to be more mechanical and less open to interpretation. Ultimately we’re not studying science exams so that we can make the best multiple choice science exam solver on Earth — we’re studying them because we’re interested in taking apart complex inference problems to understand how they work, how we can build question answering systems that automatically build explanations for their answers, and what kinds of knowledge and inference capacities we would need to make this happen. So we decided to flip the analysis upside down — instead of looking at a question and trying to figure out which of the 7 AKBC2013 question types it might be, we would instead build very detailed explanations for each question, and perform our analyses on those explanations instead.
Discretizing explanations so they can be taken apart and analyzed
There are many challenges with building a corpus of explanations in this context. One of the central issues is that we’d like to analyze these explanations for their knowledge and inference requirements, so they need to be amenable to automated analysis in some way. In order to make this happen, we “discretized” explanations into sets of (roughly) simple (atomic) facts about the world, and some collection of these facts together would then form the explanation for why the answer to a given question is correct. We further imposed more constraints, to make an automated analysis of the knowledge requirements possible:
- Simple sentences: Each “fact” in an explanation was expressed as a short, simple sentence in elementary grade-appropriate language. We tried to simplify sentences from existing resources for solving the exam (such as study guides, or simple wikipedia), but much of the time these weren’t available and we had to manually author simple sentences to suit.
- Reuse: So that we could keep track of how often the same knowledge was used across different questions, we added the requirement that if the same knowledge (fact) was used in the explanations to multiple questions, it had to be written in the exact same way, so a simple string matching algorithm could pick up each of the questions a given fact was used in. This made the annotation much more challenging to author, but is critical for the explanation-centered analysis. (In later papers, such as the WorldTree Explanation Corpus (LREC 2018), we developed tools to make this go much more quickly).
- Explicit linking between sentences in an explanation: To investigate how knowledge connects in an explanation, we also added the requirement that each fact in an explanation must explicitly “connect” to other facts in the explanation, or to the question or answer text. We did this primarily because we’re interested in studying how to combine multiple facts to perform inference, a problem sometimes called information aggregation or multi-hop inference, and a major barrier to solving inference problems. Here, in order to add this explicit linking, each sentence/fact in an explanation must share at least one word in common with the question, answer, or another sentence in the explanation. This allows the explanations to act as “explanation graphs” connected on shared words, which is the foundation upon which the more recent (and much larger) WorldTree Explanation Graph Corpus for Multi-Hop Inference (LREC 2018) was built.
Some examples of these simple explanations are shown below:
Here we can see that each simple sentence in an explanation appears to embody one kind of knowledge. I find it easier to think about these explanations visually (as explanation graphs), with the knowledge types labeled, and overlap between explanation sentences explicitly labeled. Here’s such an example, from a slide used in the talk:
We performed a detailed examination of the explanations for 212 of these questions (approximately 1000 explanation sentences) by annotating the different kinds of relations we observed, and these are summarized in the table below:
Fine-Grained Explanatory Knowledge and Inference Methods
The table above provides a fine-grained list of knowledge and inference requirements to build detailed explanations for science exam questions, and is (to me) the most interesting part of the paper. Just like the Clark et al. AKBC2013 paper, I read this table like a recipe book — if I want to be able to make a question answering system capable of answering and explaining the answers to elementary science questions, three quarters of which require some form of complex inference, these are the kinds of knowledge I have to have in my system, as well as a hint at the inference capacities required for combining that knowledge together.
There are a few parts of the table that are striking to me, that I’ll highlight:
- Proportions are wildly different when you look at an explanation-centered analysis versus a top-down analysis: The first relation in this table is taxonomic (kind-of) knowledge, which is found in 83% of explanations. But when we performed the analysis top-down (the pie-chart above), we found only about 2% of questions were testing this same taxonomic knowledge. That’s because the top-down analysis obscures many of the details of knowledge and inference requirements — it’s relatively easy to conjecture about how a question might be solved (the top-down method), but it’s also very misleading. Requiring an annotator to specify all of the knowledge required to answer a question and explain it’s answer forces a rather detailed exposition of knowledge, and that’s where the most informative content appears to be. Put another way: Using the top-down method, one might believe taxonomic knowledge unimportant, because it’s only central to answering 2% of questions. In reality taxonomic knowledge is the most prevalent form of knowledge used on this explanation-centered inference task, and likely absolutely critical to having a complete and functioning inference system.
- 21 fine-grained types: While many of the 7 AKBC types are easily visible, performing the analysis in this way, we’re able to identify much more fine-grained knowledge and inference types, as well as types (like coupled relationships, requirements, and transfers) that remained hidden in the earlier analysis.
- N-ary relations: Relations are most often extracted from text and used in question answering as triples — sets of 2-argument (X – relation – Y) tuples, as in X-is a kind of-Y (such as that a cat is a kind of mammal). What we observe here is that many relation types naturally have more arguments, as in the 5-argument “change” relation “melting (arg: who) changes a substance (arg: what) from a solid (arg: from) to a liquid (arg: to) by adding heat energy (arg: method)”, a sentence broadly applicable in questions about changes of states of matter.
This analysis is interesting, but can we use it to show some question answering models are solving more complex questions than others?
One of the natural questions one has when spending many months working on developing a new question answering model is:
“Is my ‘inference’ model actually answering more of the complex questions correctly, or is it simply doing better than the last model by answering more of the simpler questions correctly?”
Unfortunately, it’s traditionally been very challenging to answer this question — especially quickly, in an automated fashion. Here we can use the two types of annotation we’ve generated to compare a “simple” question answering system (a model that answers questions by looking at term frequency — a tf.idf model), and a particular inference solver — the TableILP solver by Khashabi et al. (2016). We can look question answering accuracy broken down using two methods — one top-down, using the 7 AKBC2013 question types, and the other bottom-up, using the 21 fine-grained knowledge types from the detailed explanations to questions.
QA Performance: Top-down
Here, the L2R model is the simpler question answering system that tries to answer questions by looking up a pre-made answer in a database. The ILP model is the TableILP inference model by Khashabi et al. (2016). The simpler model answers about 43% of questions correctly, where the ILP inference model answers about 54% of questions correctly (a gain of +11% accuracy over the simpler model, using the same knowledge). When looking at the top-down analysis (middle columns), we see that this performance gain isn’t simply from the ILP inference model answering more of the simpler (“retrieval”) questions correctly — it’s making substantial gains (up to +22%) on 3 out of the 4 complex inference type questions as well. This gives us a method of validating the inference method is doing what it’s claiming to do — answering more of the harder, inference-type questions.
QA Performance: Bottom-up
Except that I just spent quite a bit of time convincing you that the top-down analysis is much less informative than the bottom-up analysis, so let’s have a look. There’s a lot going on in this table, so let’s spend a moment to orient. The rows represent specific knowledge types identified in the fine-grained analysis. The columns represent specific models (L2R, the simpler fact-retrieval model, and ILP, the inference model) paired with specific knowledge resources (a “corpus” of study guides and simple wikipedia, or the “tablestore”, a collection of science-relevant facts). (Note that Stitch is another inference algorithm, but for simplicity I’ll focus on ILP — please see the paper for more details). The numbers in the cells of this table represent the accuracy of a given question answering system on questions whose explanation requires a given knowledge type. For example, in the first row, we see that for questions that require Taxonomic knowledge, the L2R model using the Tablestore knowledge resource answers 46% of these questions correctly. The TableILP model answers 56% of these same questions correctly, meaning the inference model shows moderate gains for these taxonomic questions. The easiest way to read this table is to look at the “Inference Advantage” column — if it’s pointing towards ILP, it means the inference model helped more on questions requiring a given knowledge type.
The take-away summary points from this table are:
- The inference model provides a substantial performance boost to the questions requiring inference knowledge. The highest gains are found in the “Inference Supporting” knowledge types, but “Complex Inference” types also show substantial gains.
- While relative gains are high, absolute performance is still low in many areas. The inference model helps almost all questions, but some questions requiring challenging kinds of inference still have a very low performance. For example, for questions requiring coupled relationships, the simpler L2R model answers only 28% of these correctly — slightly higher than chance (25% on a 4-choice multiple choice exam). The ILP inference model increases performance on these questions to 44%, which is much higher, but still one of the lowest performances. In contrast, questions requiring some types of knowledge (examples, definitions, durations) achieve between 63-70% accuracy, highlighting the relative difficulty of these questions, and providing a solid area to target in future work to boost performance.
The Overall Take-away: Inference is challenging, but we can instrument it using detailed, explanation-centered analyses
Answering (and explaining the answers to) elementary science questions is easy for most 9 year olds, but it is still largely beyond the capacity for current automated methods. Here we show that top-down methods for analyzing the knowledge and inference requirements have many challenges, limitations, and inaccuracies, and that bottom-up explanation-centered methods can provide more detailed, fine-grained analyses. This data can also be used to instrument question answering models to determine the kinds of knowledge and inference that a model performs well at, as well as identify particularly challenging knowledge and inference requirements that can be targeted to increase overall question answering performance.
Context in terms of contributions to subsequent work
This paper was critical to identifying the central kinds of knowledge and inference in standardized science exams, and has been extensively used in our subsequent work — most notably on the WorldTree Explanation Graph Corpus (LREC 2018), whose knowledge base contains many of the same types as this COLING2016 corpus, but extended to approximately 60 very fine-grained types. The paper also piloted the explanation construction analysis methodology, which has been used and refined in subsequent work. In the context of multi-hop inference, this paper also first quantified the average number of facts that need to be combined to build an explanation to an elementary science question (4 facts/question), where subsequent analyses on the larger WorldTree explanation corpus refined this to an average of 6 facts per explanation, when building explanations targeted at the explanatory detail required to be meaningful to a young child.